지우의 우당탕탕 개발일지
14-1. 고유값과 고유벡터, 삼각화 본문
1. [성질 1.] 고유값이 모두 실수의 행렬은 삼각화 가능
• 실수 정방 행렬(성분이 모두 실수의 정사각형 행렬) 중에서도 고유값이 모두 실수인 것은, 적당한 직교 행렬 을 이용함으로써 「삼각화」할 수 있는 것으로 알려져 있다.
• 삼각화란, “𝑷 ^(−𝟏)𝑨𝑷”를 계산해, 대각 성분의 좌하(혹은 우상)가 모두 제로가 되는 행렬을 만드는 작 업을 말한다. 예를 들면 이런

* n차고유다항식의 해는 실수해, 중복해, 허수해를 갖는다.
2. 삼각화란
• 삼각 행렬이란 대각 성분보다 좌하 또는 우상의 성분이 모두 0의 행렬을 말한다.
• 특히, 왼쪽 하단이 모두 0인 행렬은 상단 삼각 행렬, 오른쪽 상단이 모두 0인 행렬을 하단 삼각 행렬 이라고 한다.
• 위의 예는 상단 삼각 행렬이다. 삼각 행렬은 성분의 거의 절반이 0으로 구성되어 있다.
• 따라서 삼각 행렬을 포함하는 수식은 계산이 편하고 선형 대수를 실용하는데 중요한 역할을 한다.
3. 행렬의 삼각화
• 모든 정방 행렬은, 적당한 정칙행렬 𝑷 를 가지고, 𝑷 ^(−𝟏)𝑨𝑷 를 삼각 행렬(상삼각 행렬)로 할 수 있다.
이와 같은 해서 삼각 행렬을 만드는 것을 삼각화라고 한다.
즉 임의의 정방 행렬 𝑨에 대해서, 다음 식이 성립하는 적절한 정칙 행렬 𝑷가 존재한다.

• 단, 대각 성분 𝒂𝟏𝟏, 𝒂𝟐𝟐, … , 𝒂𝒏𝒏은 𝑨의 고유값이다. 이렇게 삼각 행렬(위 삼각 행렬)을 만드는 것을 삼각화라고 한다.
• 대각화에 관한 설명 중에서 대각화할 수 있는 것을 나타내는 대각화 가능이라는 말이 있었다.
• 한편, 삼각화는 정방 행렬인 것만으로 절대적으로 할 수 있으므로, 삼각화 가능이라는 말은 없다.
• 또한 삼각화 그 자체는 하단삼각 행렬을 만드는 것도 해당이 되지만, 상반부 행렬을 만드는 것이나 하반부 행렬을 만드는 것이나 본질적으로 큰 차이는 없기 때문에 선형 대수 수업 중에서는 간단하기 때문에 상반부 행렬을 만드는 것에 한정하는 경우가 대부분입니다.
• 모든 정방 행렬에서 삼각화할 수 있는 것은 수학적 귀납법을 이용하는 것으로 증명이 가능하다.
• (이에 관한 증명은 생략함)
4. 직교 행렬을 이용한 삼각화
• 임의의 정방 행렬은, 어떤 정칙 행렬을 이용해 삼각화할 수 있지만, 특히, 정방 행렬의 고유치가 모두 실수인 경우는, 직교 행렬(전치가 역행렬이 되는 정칙 행렬)로 삼각화 수 있다.
• 덧붙여서, 정방 행렬의 고유값(치) 중에 복소수가 포함되는 경우, Unitary행렬(유니터리행렬)이라고 하 는 행렬을 이용하는 것으로 삼각화할 수 있다.
• 유니터리 행렬이란 쉽게 말하자면 복소수 버전의 직교 행렬 같은 존재이다.
• 구체적으로는, 어느 행렬을 전치해, 모든 성분을 컬레 복소수(허수 부분의 부호를 바꾼 복소수)로 옮 겨서 행한 행렬(수반 행렬이라고 합니다)이, 어느 행렬의 역행렬이 되는 행렬입니다.(뒤에서 구체적 으로 다룸)
5. 삼각화의 구체적인 방법
• 실제로 삼각화하는 것은 매우 귀찮은 작업이다.
• 그리고 실용적인 측면에 있어서는, 삼각 행렬보다 더욱 간단하고 편리한 조르단 표준형(근사 대각화) 이라고
하는 형태를 만드는 것이 많기 때문에, 실제로 삼각화를 실시하는 경우는 그다지 많지 않다.
• 그럼에도 불구하고 삼각화 방법을 알아 두면 좋은 면이 있음.
삼각화의 방법은 대체로 다음과 같다.
1. 고유값 및 고유 벡터를 구하자.
2. 특정 고유 벡터와 직교한 벡터를 모으자.
3. 벡터 크기를 1로 정렬하자.
4. 오른쪽 상단을 제외한 소행렬에 동일한 작업을 수행한다.
5. 모든 P를 곱한다.
6. 삼각화의 구체적인 방법의 예
다음과 같은 행렬을 예로 삼각화를 해보자.
이 행렬은 차수가 3인데, 고유벡터는 2개밖에 없기 때문에 대각화는 할 수가 없다.

1. 고유값 및 고유 벡터를 구하자
• 앞에서 학습한 방법으로 고유값과 고유벡터를 구할 수있다. 여기서 계산 과정은 생략한다.
• A의 고유값은 2와 -1이며, 각각에 해당하는 고유 벡터 중 하나는 아래에 나열된 대로이다.

2. 특정 고유벡터와 직교한 벡터를 모으자
• 고유 벡터 중에서 하나 선택해서 이 고유 벡터를 포함 하는 동시에 서로 직교하는 차수개의 벡터를 준비한다.
• 여기서는 3차원 행렬을 다루고 있으므로 3개의 벡터 쌍을 준비한다. 직교하는 벡터는 적당히 찾아 보자.
물론 간단한 고유 벡터를 선택하는 것이 유리하다

3. 벡터의 크기를 1로 해서 정렬한다.
• 벡터 조합은 길이가 일정하지 않기 때문에 적당히 스칼라 배로 해서 길이를 1에 정렬한다.

• 벡터의 모양을 보면 알 수 있겠지만 선택한 고유 벡터에 기초해서 정규 직교 기저를 만들고 있는 것이다.
• 정규 직교 기저가 생기면, 이것들을 나열해서, 이것들을 열 벡터로 하는 행렬을 만들어 보자.

• 일단 이것이 𝑷 ^(−𝟏)𝑨𝑷 의 𝑷 후보가 된다.
4. 오른쪽 상단을 제외한 한 차수 작은 행렬에 대해서 동일한 작업을 반복한다.
• 먼저 위에서 구한 𝑷𝟏을 사용하여 𝑷𝟏 −𝟏𝑨𝑷𝟏을 계산해보자. 이 계산과정은 여기서는 생략

• 어떤 경우에는 이 시점에서 상삼각 행렬이 완성될 수도 있다.
여기서는 아직 삼각화가 완료되지 않은 경우이기 때문에,
다음은 𝑨𝟏의 상단 행과 좌단 열을 제거한 다음의 소행렬에 대해 이전과 마찬가지 작업을 수행한다.

• 이 행렬의 고유값은 최초 행렬의 고유값으로부터 선택한 고유 벡터에 대응하는 고유값을 제외한 것이다.
• 최초 행렬의 고유치는 2와 -1이었지만 실제로는 2는 중복해 2이었기 때문에 고유값은 2,2, -1의 3개이다.
여기 에서 2를 1 하나만 제외하고 남은 2와 -1이 𝑨𝟐의 고유값이 된다. (실제로 𝑨𝟐의 고유 방정식을 풀면 확인할 수 있다

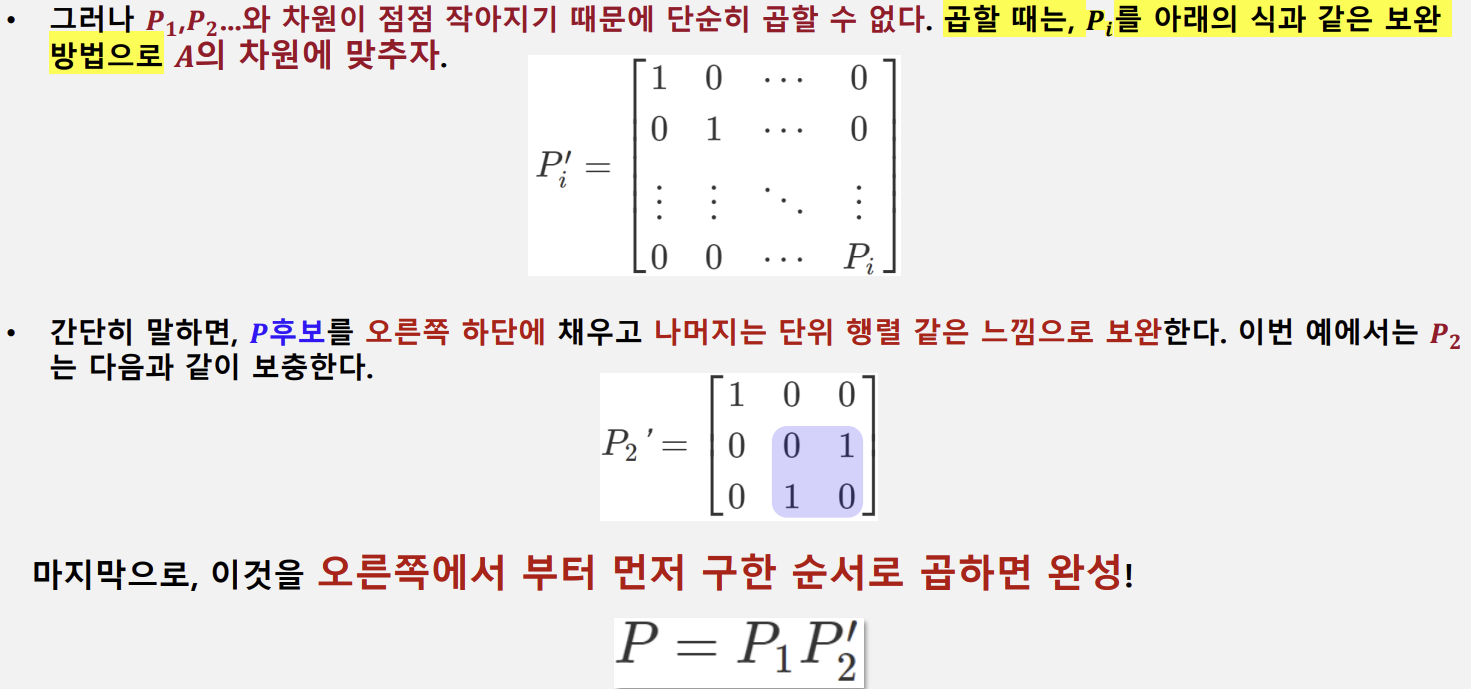
5. 모든 P후보를 곱한다.
• 삼각화가 성공한 시점에서 𝑷𝟏과 𝑷𝟐라는 두 개의 𝑷후보가 등장했다 (차수가 많으면 𝑷𝟑 이후도 계속된다 …).
• 마지막으로, 이들을 곱하여 𝑷자체를 만들어 보자

7. 성질2. 실수 대칭 행렬의 고유값은 모두 실수


8. 대각화가 가능한 이유

9. 직교 행렬이 대각화할 수 있는 것은 대칭 행렬뿐!


10. 직교행렬에 의한 대각화의 필요 충분조건

'CS > 선형대수학' 카테고리의 다른 글
| 14주차-2. 선형변환 (0) | 2023.12.14 |
|---|---|
| 13주차.고유값과 고유벡터 (0) | 2023.12.14 |
| 12주차. 벡터의 외적 (0) | 2023.12.14 |
| 12주차. 벡터의 내적 (0) | 2023.12.14 |
| 11주차. 벡터 공간-2(생성/기저/차원) (0) | 2023.12.14 |



