지우의 우당탕탕 개발일지
13주차.고유값과 고유벡터 본문


1. 고유값과 고유벡터란 무엇인가
2. 고유값과 고유벡터는 무엇에 도움이 되는가
3. 간단한 예로 이해하기
4. 고유값(치) 문제란
5. 고유값과 고유벡터를 구하는 방법
6. 고유방정식으로 고유값(치)를 구함
7. [문제풀기] 고유값문제 풀어보기
8. 대각합(trace)의 의미와 고유값(치)의 관계
9. 고유다항식
10. 고유다항식의 계수 구하기 + 증명
11. 대각합과 고유치 + 예제
12. 행렬식과 고유값 + 간단한 증명
13. 대각화란?, 행렬의 대각화와 대각화 가능
14. 대각화의 편리한 점
15. 고유값과의 관계
<대각화와 고유값/고유벡터>
16. 대각화가능의 조건
<대각화 가능 조건에 관한 정리>
<이 정리로부터 대각화 가능인가를 알아보기 위해서는>
17. 대각화하기
18. 대칭행렬의 대각화의 성질
19.대칭행렬
20. 직교행렬
21. 대칭 행렬은 직교 행렬로 대각화할 수 있다! ?
1. 고유값과 고유벡터란 무엇인가
1) 행렬 A에 의한 선형변환

=> 이것을 행렬 A에 의한 선형변환이라고 함.
선형변환을 하면 거의 모든 벡터는 행렬 A와의 행렬곱에 기초해서 다른 별도의 벡터로 변화한다.
그러나, 그 중에서 벡터의 크기만 변할 뿐, 방향은 일절 변화가 생기지 않는 벡터가 존재할 수 있다.
여기서 방향이 변하지 않는 특별한 벡터 x를 고유벡터라 하고,
변환후에 있어서 벡터의 크기의 변화률

고유값(치)라고 한다.

2. 고유값과 고유벡터는 무엇에 도움이 되는가
고유값과 고유벡터는 어떤 행렬을 이용한 선형변환의 특징을 나타내는 지표의 하나인다.
• 검색엔진 알고리즘(Google의 PageRank)
• 통계학(주성분 분석 방법등에)
• 양자 역학(시간에 의존하지 않는 슈레딩거 방정식)
등에 활용
3. 간단한 예로 이해하기
[ i ]
step 1) 2차원 정방행렬 A
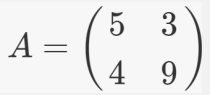
step2) 아무런 별 다른 것이 없는 벡터 x를 선형변환하기


위의 결과와 같이 전혀 다른 방향의 벡터가 생성된다.
고유벡터 이외의 대부분의 벡터는 선형변 환을 통해서 이와 같은 거동을 하게 된다
[ ii. 고유벡터가 주어졌을 때 ]


어떻게 되었는지 살펴보면, 변환후의 벡터는 변환전과 방향은 변하지 않았다는 것을 알 수 있다.
길이는 3배가 되었지만, 이 변화률 “3”은 행렬 A의 고유값 중에 하나이다
[ iii ]

4. 고유값(치) 문제란

5. 고유값과 고유벡터를 구하는 방법
• 고유값(치) 문제를 푸는 방법 중의 하나가 고유방정식(특성방정식이라고도 함)이라는 것을 푸는 방법이다.
Step 1) 고유방정식 (특성방정식) 풀어서 고유값을 유도함

Setp2) 고유값에 대한 고유벡터를 유도함

고유벡터는 하나의 고유값(치)에 대해서 무수히 있을 수 있다(어떤 해의 스칼라 배도 해가 되기 때문에). 고 유값 벡터를 구하는 문제에 대해서 특별한 내용이 없는 한 임의의 변수을 스칼라 배한 형태로 기술한다.
6. 고유방정식으로 고유값(치)를 구함
• 먼저, 어떤 고유값(치) 에 대한 고유벡터를 구하는 문제는 아래의 식을 만족하는 을 구하는 문제이다.

• 이 식은, 첫번째로 양변의 왼쪽에 단위행렬 E 을 곱하고, 두번째로 우변을 좌변으로 이항하면 다음과 같은 형태가 된다.


• 고유벡터가 존재하기 위해서는 이 연립방정식이 비자명해를 갖지 않으면 안된다.
(자명해=영벡터는 고유 벡터로 취급하지 않기때문에)
• 이를 위한 조건은 행렬 의 행렬식이 0 이 되어야 한다는 것.
즉 역행렬이 존재하지 않는 것이다.
• 만약에 역행렬이 존재하면, 연립방정식의 왼쪽에 역행렬을 곱하면 x=0 이 도출된다.
이것은 영벡터의 이외의 해가 존재하지 않는 것이 된다.
(𝐴 − 𝜆𝐸) 𝑥 = 0
(𝐴 − 𝜆𝐸) = 𝑊

=> 𝐼𝑥 = 0 , 𝑥 = 0
7. [문제풀기] 고유값문제 풀어보기
Step1. 고유방정식을 풀자
2차원 정방행렬 A



Step2. 각 고유값(치)에 대해서 고유벡터를 도출하자.



8. 대각합(trace)의 의미와 고유값(치)의 관계
1) 대각합(trace)

2) 고유다항식

9. 고유다항식
고유다항식 이란?

10. 고유다항식의 계수 구하기 + 증명
고유다항식을 전개하면, 굉장히 힘든 계산 상황이 전개될지도…
그러나. 일부 항의 계수라면 어느 정도 알 수 있을 것이다. 실은 행렬식의 성질로 부터

( “𝑡 𝑛 “ “𝑡 𝑛−1 ” )
의 계수이면 간단하게 구할 수 있다.
(1) t^n의 계수
• 이것은 대각 성분을 모두 곱한 것으로 다음과 같은 다항식
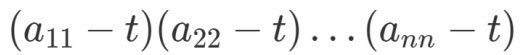
에 있어서 𝒕 ^𝒏계수와 같다. 여기서 계수는 “ (−𝟏)^ 𝐧” 이다.

(2) t^(n-1)의 계수
• 이것도 대각 성분을 모두 곱한 다음의 다항식으로 부터 구할 수 있다.
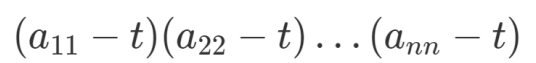

[증명]



11. 대각합과 고유값의 사이의 관계


[ 예제 ]
1) 2차원 정방행렬

12. 행렬식과 고유값 + 간단한 증명
행렬식과 고유값 사이의 관계

[증명]

13. 대각화란?, 행렬의 대각화와 대각화 가능
행렬의 대각화와 대각화 가능
어떤 정방 행렬 𝑨에 대해서 적절한 정칙 행렬 𝑷를 이용해서 곱 𝑷 ^(−𝟏)𝑨𝑷 이 대각 행렬이 될 수 있다.
이와 같이 대각 행렬을 만드는 과정을 대각화라 하고, 대각화할 수 있는 𝑷가 존재하는 것을 대각화 가능이라고 한다.
• 어떤 정방 행렬 𝑨에 대해서 다음 식이 성립하는 정칙 행렬 𝑷를 존재할 때 𝑨는 대각화 가능이라고 한다.

• 또한, 이렇게 대각행렬을 만드는 것을 대각화라 한다.
14. 대각화의 편리한 점
• 대각화의 이점(장점) 중 하나는 행렬의 𝒏승 계산에 매우 유용하다는 것이다.
• 대각 행렬의 𝒏승은 원래의 대각 성분의 𝒏승을 성분으로 갖는 대각 행렬이 된다.
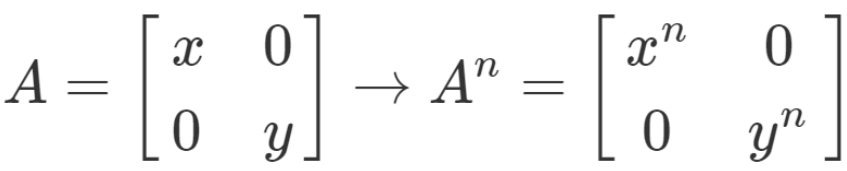
• 따라서 행렬의 n승을 계산할 때는 대각화를 해서 대각행렬의 n승을 구하는 것이 편리하다.

15. 고유값과의 관계
<대각화와 고유값/고유벡터>
• 대각화라고 하는 과정에는, 행렬의 고유값·고유벡터가 중요하게 등장한다. 그 이유는 예로 2차 정방 행렬이지 만 어떤 차원이라도 상관없다.
• 먼저 대각화 가능한 2차 정방 행렬 𝑨를 이용해서, 𝑨는 어떤 2차 정칙 행렬 𝑷 = (𝒑𝟏𝒑𝟐)를 사용하여 다음과 같 이 대각화할 수 있다.

간단하게, 이것을 변형하면 된다. 먼저, 위의 식에서 양변에 𝑷를 곱하면

• 대각화에 의해서 만들어진 대각행렬 성분, 그리고 대각화에 이용된 𝑷의 열 벡터에는 어떠한 관계가 있다.

가 성립할 때
𝑷 = (𝒑𝟏,𝒑𝟐, … 𝒑𝒏) 로 하면, 성분 𝒂𝟏 ~ 𝒂𝒏는 각각 행렬 A의 고유값이고,
열벡터 𝒑𝟏 ~ 𝒑𝒏 는 고유값 𝒂𝟏 ~ 𝒂𝒏에 각각 대응하는 고유벡터이다
16. 대각화가능의 조건
<대각화 가능 조건>
• 대각화는 모든 정방 행렬에서 가능하다고 한정할 수 없다. 그러나 다음과 같은 조건이 성립하면 대각화를 할 수 있다.
<대각화 가능 조건에 관한 정리>
𝒏차 정방 행렬 𝑨에 관해서 다음 명제가 성립한다.
𝑨는 서로 1차(선형)독립인 고유벡터를 𝒏개 가진다 ⇔ A는 대각화 가능
<이 정리로부터 대각화 가능인가를 알아보기 위해서는>
1. 고유값을 구한다
2. 대응하는 고유벡터를 구한다.
3. 차수와 동일한 수의 고유벡터가 서로 1차독립인가를 알아본다.
이 3가지 단계를 통해서 알 수 있다.
17. 대각화하기



18. 대칭행렬의 대각화의 성질
< 대칭 행렬의 대각화의 성질과 반드시 대각화할 수 있는 이유 >
행렬의 대각화는 모든 행렬에서 할 수 있는 것은 아니다.
그러나 대칭 행렬을 상대로 한다면 반듯이 대각화할 수 있다.
그럼 “대칭 행렬”의 대각화에 초점을 맞추고 그 성질 등을 알아보자
19.대칭행렬
전치해도 자기 자신의 행렬이 되는 행렬


원래 행렬의 성분은 실수이거나 복소수(허수 i를 포함한 수)이거나
하지만, 여기에서는 실수의 성분 만을 가지는 행렬을 취급한다.
실수만을 성분으로서 가지는 행렬을 특히 실대칭 행렬이라고 한다.
20. 직교행렬
직교 행렬은 전치와의 곱이 단위 행렬 𝑬가 되는 행렬이다.

즉, 전치가 역행렬 그 자체인 행렬을 말한다.

21. 대칭 행렬은 직교 행렬로 대각화할 수 있다! ?
• 그런데, 행렬의 대각화는, 반드시 모든 행렬로 할 수 있는 것은 아니다. 그러나 대칭 행렬이라면 직교 행렬을 사용하여 절대적으로 대각화 할 수 있다.
• 직교 행렬로 대각화할 수 있는 이유는, 행렬이 가지는 다음의 2개의 성질을 조합해 설명할 수 있다.
1. 고유값이 모두 실수인 행렬은 삼각화 가능
2. 실대칭 행렬의 고유값는 모두 실수
'CS > 선형대수학' 카테고리의 다른 글
| 14주차-2. 선형변환 (0) | 2023.12.14 |
|---|---|
| 14-1. 고유값과 고유벡터, 삼각화 (0) | 2023.12.14 |
| 12주차. 벡터의 외적 (0) | 2023.12.14 |
| 12주차. 벡터의 내적 (0) | 2023.12.14 |
| 11주차. 벡터 공간-2(생성/기저/차원) (0) | 2023.12.14 |



