벡터의 개념의 이해
1. 벡터의 개념과 표현
1) 벡터의 개념과 표기법
2) 평면상의 벡터
3) 벡터의 크기와 기하학적 표현
4) 단위벡터와 단위좌표벡터 //여기까지
2. 벡터의 연산
1) 벡터의 합과 차
2) 벡터의 스칼라 곲
3) 벡터의 성질
4) 벡터의 응용
=> 벡터의 연산은
9주차. 벡터의 개념과 표현2(벡터의 합과 차/스칼라곱/성질/응용)
2. 벡터의 연산 1) 벡터의 합과 차 2) 벡터의 스칼라 곲 3) 벡터의 성질 4) 벡터의 응용 1) 벡터의 합 : 두 벡터를이어 붙이기 1-2) R^n상에서의 벡터의 합 2) 벡터 합의 교환 법칙 예제) 3) 벡터의 차 4)
erase-jeong.tistory.com
여기에~
1. 벡터의 개념과 표현
* 개념 이해
* 스칼라 -> 크기
* 벡터 -> 크기 + 방향

* 벡터는 선형 세상에서 다를 수 있는 기본 개념과 표현의 도구이다.


1) 벡터의 의미
수 또는 기호를 1차원 배열로 표현한 것

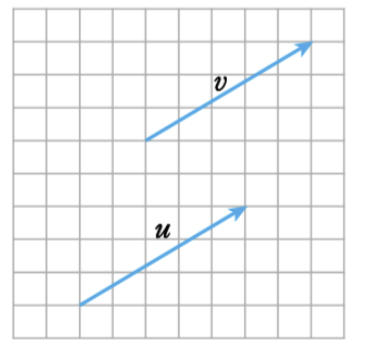
2) 방향과 크기가 있는 물리량을 나타내는 벡터
위치와 무관하게 벡터의 방향과 크기가 같으면 동일한 벡터
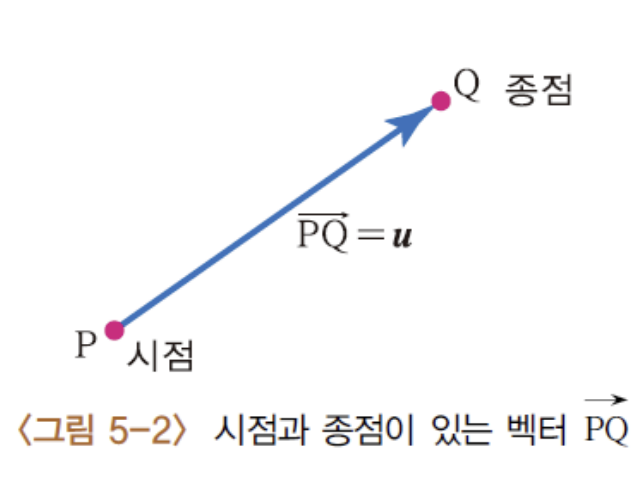
3) 시점, 종점, 유향성분
▪ 화살표의 시작점인 P를 시점(initial point, tail)이라고 하고,
▪ 끝나는 점인 Q를 종점(terminal point, head)이라고 한다.
▪ 점 P에서 점 Q까지의 방향을 가진 선분 PQ를 유향선분(directed segment)이라고 한다
4) 벡터의 표현 (예시)
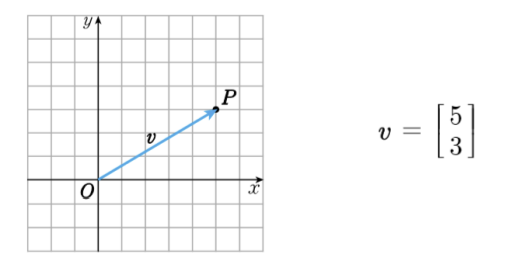
- 시작점과 끝 점이 있는 선분을 나타내는 벡터

- 좌표공간상의 위치를 나타내는 벡터
5) 벡터의 표현2

도형을 이용한 벡터의 표현은 화살표로 나타내는데,
이때 그 화살표의 길이가 벡터의 크기가 되고,
화살표가 가리키는 방향이 벡터의 방향이 됩니다
6) 벡터의 표기법
벡터는 다음과 같이 굵은 활자체나 보통문자 위에 화살표를 붙여 표기합니다.
a, b, c, ......, A, B, C, ...... 혹은
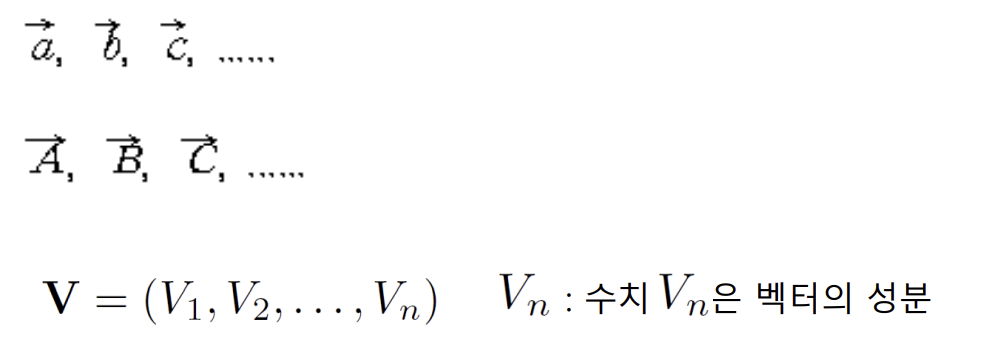
cf) 스칼라 표기 : a, b, c, ......, A, B, C, ...... 와 같이 보통문자로 표기함
7) 벡터의 다양한 관점 정리
skip
8) 좌표 표현법
단순히 그림만 그리면 제 3자에게 전달하기 힘듦.
따라서 미리 기준선을 만들어놓고 여기에 벡터를 그리면 편함.
이때 기준선을 "좌표축(axis)" 라고 함.
좌표축들이 만나는 점을 "좌표원점(origin)" 이라고 함.
이 둘을 함께 "좌표계(coordinate system)"라고 함.

보통 좌표축들은 x,y,x 등으로 표기
좌표원점 : o으로 표기
ex) 2차원 벡터 A를 2차원 직교 좌표계에 표현한 것

9) 좌표 표현법 - 변환
• 이 좌표 표현법에서 좌표계의 선택은 유일한 것이 아니다.
하나의 추상적 벡터를 표현함에 있어 얼마든지 많은 좌표계에서 표현할 수 있는데, 이는 마치 실제 개체를 일상적 언 어로 표현할 때 어떤 언어를 선택하던 무관한 것과 같은 이치이다.
• 가령, 연필이라는 개체를 놓고 우리는 "연필"이라 하고, 영어에서는 "pencil"이라 하는데, 이 두 표현이 모두 맞는 표현입니다.
• 또한 생각해야 할 점은 동일한 개체를 다른 언어로 표현했을 때, 그 두 표현 간에는 번역이 가 능하다는 점입니다. 서로 다른 언어간에 번역에 필요한 것이 사전입니다.
• 이와 마찬가지로 수학에서도 동일한 수학적 개체를 다른 좌표계에서 표현했을 때, 그 두 표현 간에는 번역이 가능합니다. 수학에서 이러한 표현과 표현간의 번역으로 변환(transformation) 이라 합니다.
10) 벡터의 성분
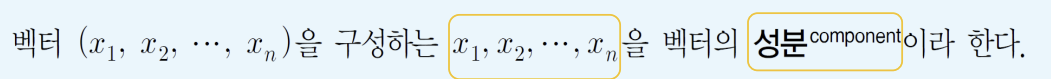
• 벡터를 응용하고자 할 때에는 시각적인 경우보다 수학적인 식 으로 표현하는 것이
알고리즘을 개발하는 데 있어 더욱 손쉽게 다룰 수 있음.
• 벡터를 해석학적으로 표현해 보면 일반적으로 벡터는 a는 실수 들의 순서쌍 a=(a1 ,a2 )입니다.
• 스칼라 a1 ,a2 를 각각 벡터 x성분, y성분이라 합니다.
• 벡터 a는 반듯이 위치 벡터일 필요는 없습니다.
• 벡터 a=(a1 ,a2 )를 2차원 평면에서 기학적으로 표현하면 왼쪽 상 단의 그림과 같습니다.
• 왼쪽 하단 그림에서 점(x,y)와 점(x+4, y+3)사이의 변위를 (4,3) 으로 씁니다. 그리고 (4,3)의 위치벡터는 원점에서 시작하여 점 P(4,3)을 종점으로 하는 벡터 입니다.
11) 2차원 벡터, 3차원 벡터, n차원 벡터
2개의 성분을 갖는 벡터는 2차원 벡터, 3개의 성분을 갖는 벡터는 3차원 벡터, n개의 성분을 갖는 벡터는 n차원 벡터라고 한다.

12) 위치벡터(position vector)
벡터는 좌표로도 나타낼 수 있는데 가령 3차원 공간에서 원점(0,0,0)으로부터 좌표상의 위치(x,y,z)까지 향하는 벡터를 위치벡터라고 부른다.

• 벡터의 시점은 평면 또는 공간 내의 어떠한 점을 잡아도 좋으나, 보통 원점을 시점으로 하는 벡터를 주로 사용.
• 원점을 시점으로 하고 점 P를 종점으로 하는 벡터를 점 P의 위치벡터(Position vector)라 함.
• 그리고 시점을 고정되지 않은 벡터를 자유벡터(Free Vector)라 함
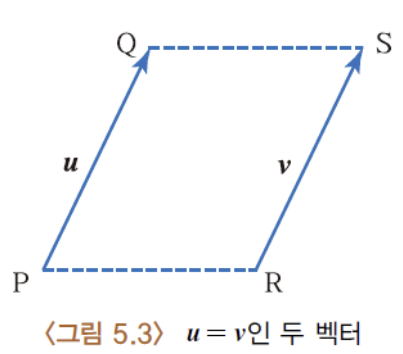
13) 벡터의 동치


⚫
두 벡터 PQ와 RS가 똑같은 크기와 방향을 가지면,
이 두 벡터가 어디에 위 치해 있더라도 서로 동치(equivalent)라고 한다.
⚫
이와 같이 벡터의 시점과 종점의 위치에 관계없이 크기와 방향만을 생각할 때
이것을 기하벡터(geometric vector)라고 부르며 u = v로 나타낸다
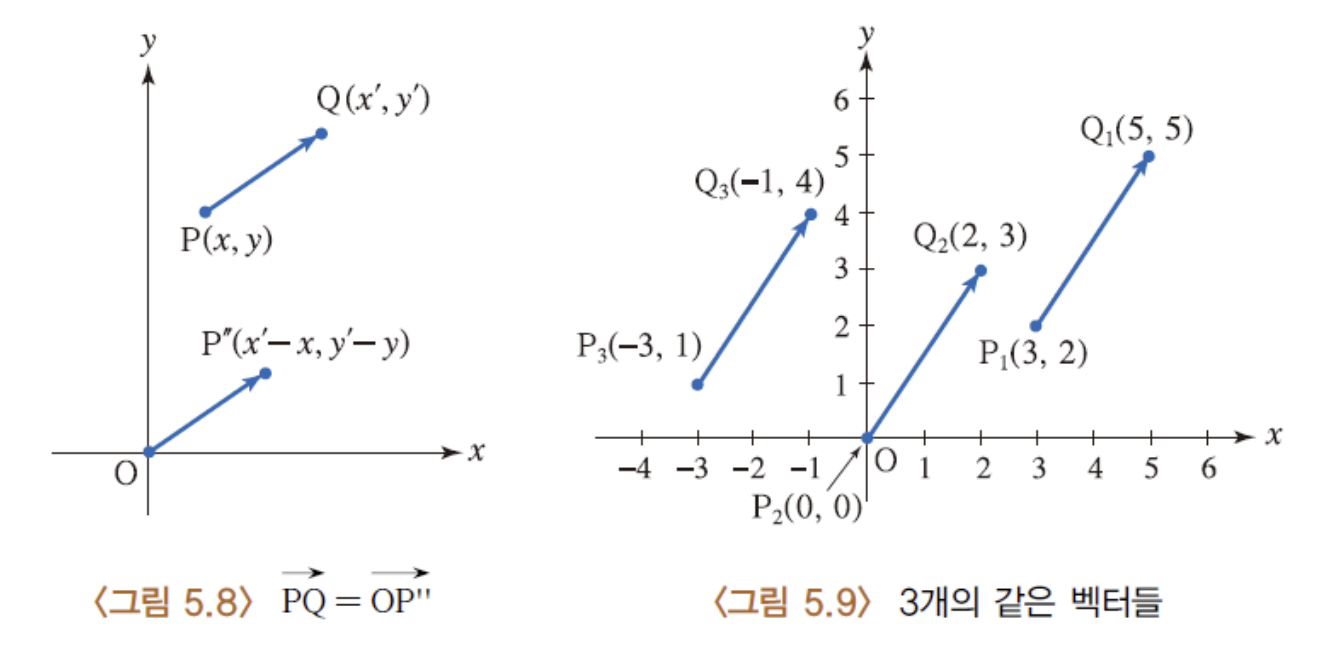
14) 벡터의 동치 - 예시



15) 영벡터
영벡터(zero vector, null vector) : "모든 성분이 0인 벡터"

<정리>
Q.
좌표상으로 보면 두 벡터가 분명히 다른데, 두 벡터가 같다라는 말은 잘 이해가 안돼요.

A.
벡터에서는 크기와 방향이 같은지를 중요하게 생각함.
크기와 방향이 같은 두 벡터는 평행이동시키면 사실상 같은 벡터가 됨.
=> 벡터의 표기를 보면 행렬의 표기법과 비슷함. 행렬의 열벡터나 행벡터의 표기법과 같음
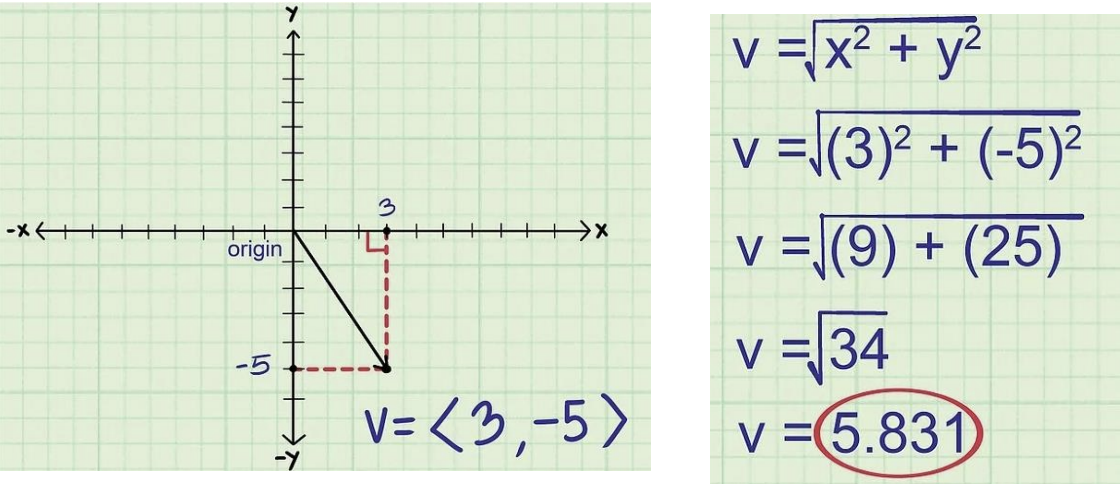
16) 벡터의 크기, 길이, 노름(norm)


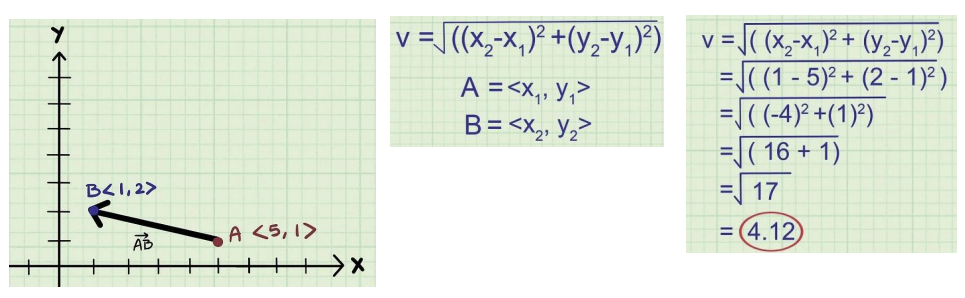


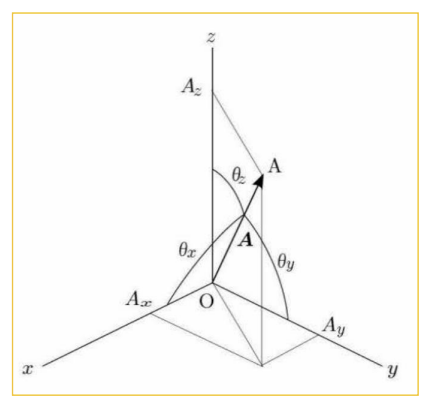
17) 3차원 벡터의 크기와 방향
(i) 벡터의 크기

(ii) 벡터의 방향

18) 단위벡터(Unit vector)


• 어떤 벡터의 단위벡터는 간단하게 말하면 “방향이 변하지 않고 강제 적으로 크기가 1로 변환한 벡터"이다.
• 단위 벡터의 정의: 𝒂벡터와 같은 벡터의 방향을 가지고 크기가 1인 벡터
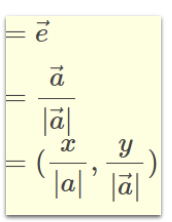

19) 단위벡터 예제


20) Q. 스칼라 0과 벡터 0은 차이점은?

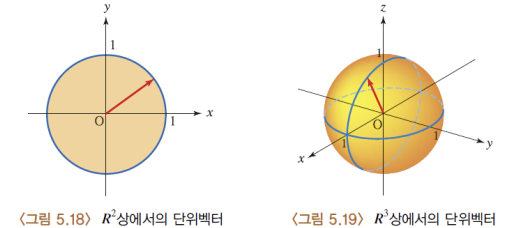
21) R, R^2, R^3, R^n 의 차이점은?


22) 단위좌표벡터 (Unit coordinate vector) , 기저벡터 (basis vector)
⚫ R2상에는 다른 벡터들을 편리하게 나타낼 수 있는 두 개의 특별한 벡터인 단위좌표벡터(Unit coordinate vector)가 있다 ⚫ 두 벡터 i와 j를 벡터공간 R2의 기저벡터(basis vector)라고 한다
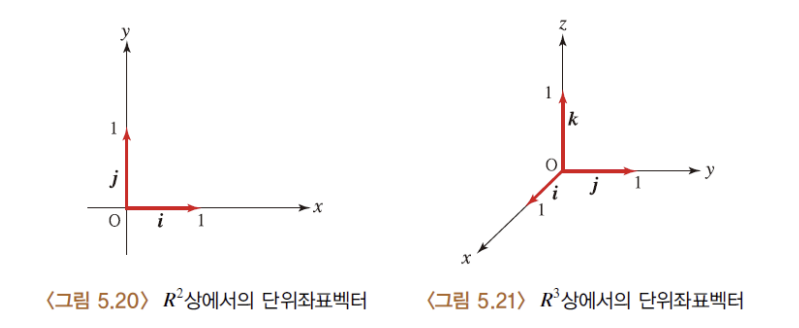
선형대수학에서, 어떤 벡터 공간의 기저(基底, 영어: basis)는
그 벡터 공간을 선형생성하는 선형독립인 벡터들이다.
달리 말해, 벡터 공간의 임의의 벡터에게 선형결합으로서 유일한 표현을 부여하는 벡터들이다.
22) 벡터의 선형성
- 함수(사상)와 벡터가 선형이다, 선형성을 가진다는 의미는 다음과 같이 정의한다

• 두벡터의 합을 입력하였을 때, 출력 값은 각 각 두 벡터를 함수로 입력했을 때의 출력값의 합과 같다 것이고
어떤 벡터의 k배를 해서 출력을 시킨 결과는 그냥 벡터를 출력한 뒤 k배를 한 것과 결과가 동일하는 것이다.
• 이와 같은 간단한 조건을 만족시키는 것을 선형이라고 함. 단. 선형이라는 표현이 항상 직선과 일치하지 않음
• 직선은 일차 함수의 형태로 표현되는데, 모든 일차 함수가 선형성을 가지는 것이 아님,
원점을 지나는 직 선함 선형성을 가짐

23) 선형 독립



24) 선형 결합 (일차 결합, Linear Combination)
벡터들의 스칼라배들이 합으로 연결된 형태

선형결합은 각각의 벡터들 앞에 스칼라 배를 해서 합으로 표현하는 모양
25) 선형 생성 (Span)
벡터 공간의 V의 부분집합 합 S!=0 에 대하여 S에 속한 벡터를 사용하여 만든 모든 선형결합(일차결합)의 집합을 S의 생성공간(Span)이라고 함. span(S)로 표기
26) 정리
단위벡터, 단위좌표벡터, 기저벡터
- 단위벡터는 크기가 1인 벡터를 말한다.
- 단위좌표벡터는 좌표상의 단위벡터임을 강조한 것이다.
- 기저벡터인 i, j, k 등도 단위벡터 중의 하나인데, x,y,z 상의 축의 역할을 담당한다.
- 기저벡터란 n차원 공간에서 임의의 벡터를 표현할 수 있는 기준이 되는 벡터이다.
- n차원(R^n) 에서는 n개의 벡터가 있어야 기저 벡터가 이루어지며,
- 또한 벡터가 서로 선형독립적이거나 행렬식이 0이 되지 않아아 기저 벡터이다.
27) 단위좌표벡터 구하기

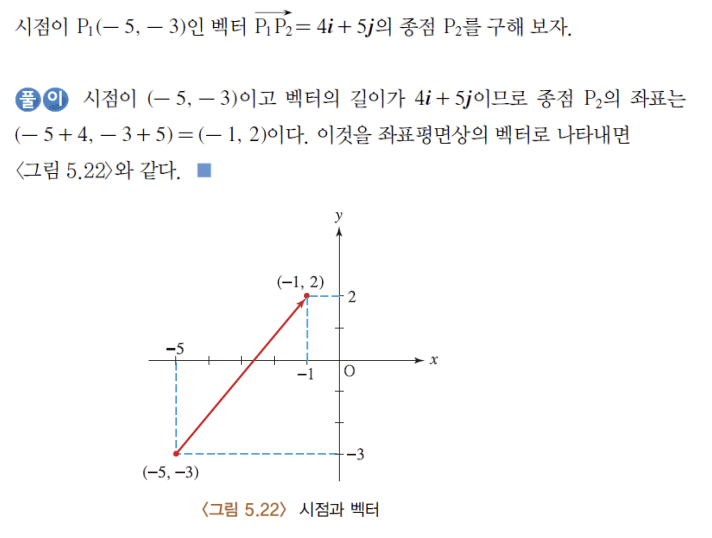
28) 시점으로부터 종점 구하기
'CS > 선형대수학' 카테고리의 다른 글
| 선대 10주 . 벡터공간에 대한 개념 이해 (0) | 2023.12.14 |
|---|---|
| 9주차. 벡터의 개념과 표현2(벡터의 합과 차/스칼라곱/성질/응용) (0) | 2023.12.14 |
| 8-2) LU 분할(분해) 법 (0) | 2023.10.22 |
| 8) 크레머 공식 (0) | 2023.10.22 |
| 7) 선형방정식의 해법과 응용 (0) | 2023.10.22 |

