9주차. 벡터의 개념과 표현2(벡터의 합과 차/스칼라곱/성질/응용)

 

2. 벡터의 연산     1) 벡터의 합과 차      2) 벡터의 스칼라 곲      3) 벡터의 성질      4) 벡터의 응용

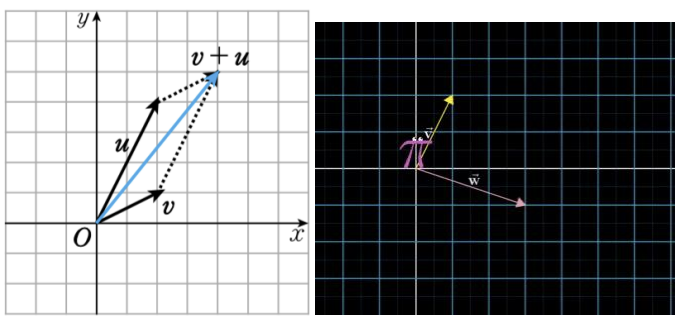
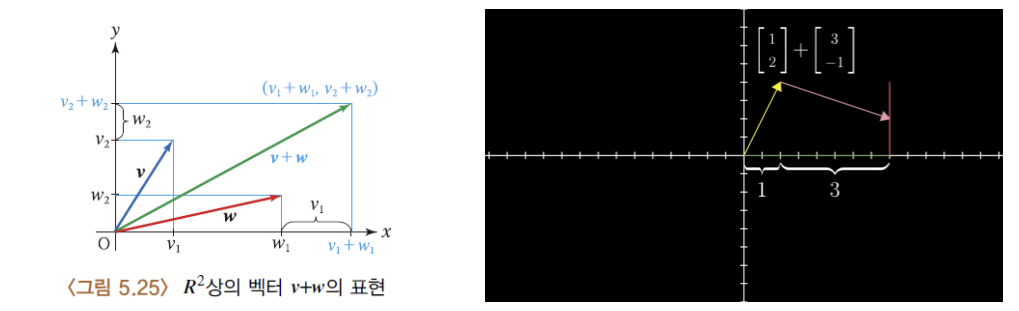
1) 벡터의 합

: 두 벡터를이어 붙이기

 

 

 

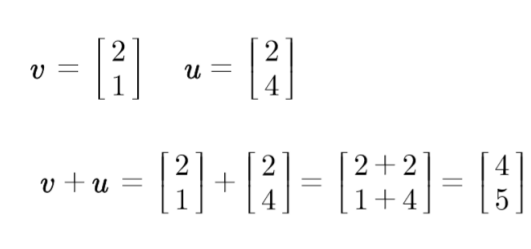
1-2) R^n상에서의 벡터의 합

 

 

 

---

 

 

 

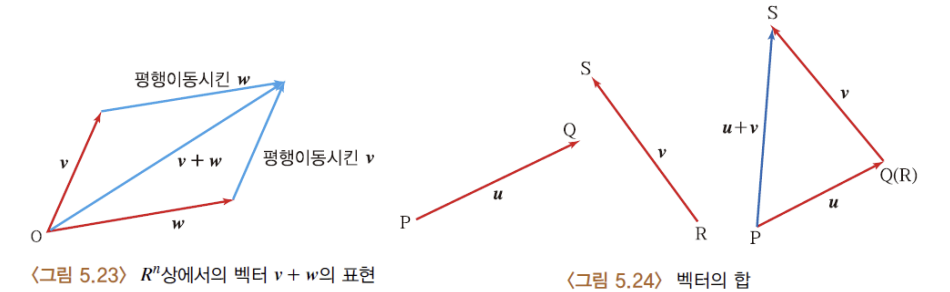
2) 벡터 합의 교환 법칙

 

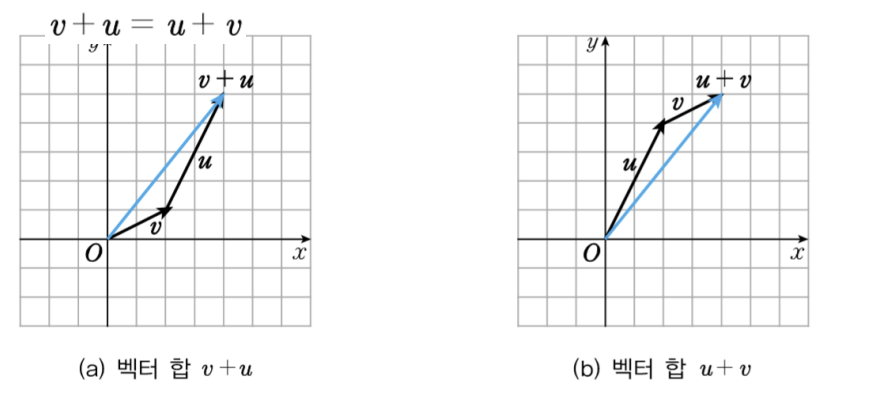
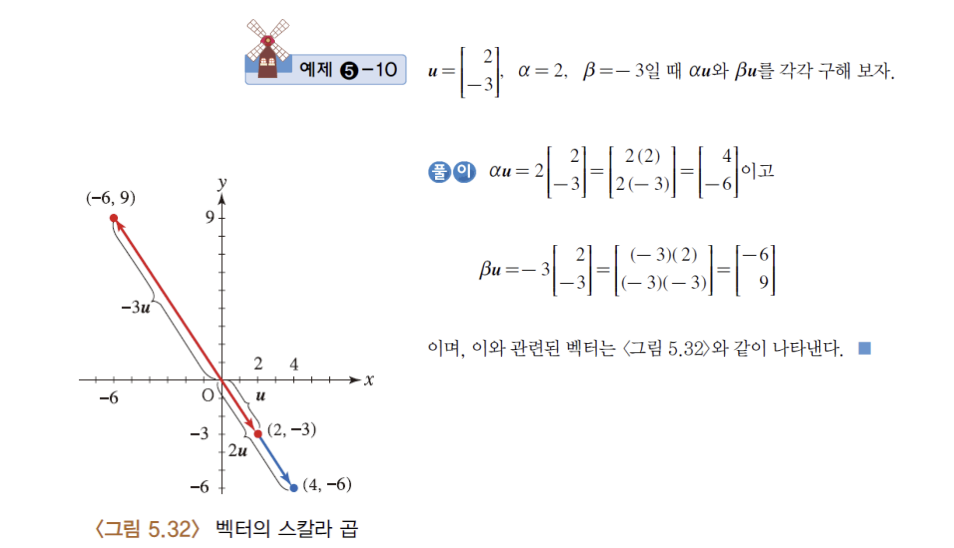
예제)

 

 

 

 

3) 벡터의 차

 

 

 

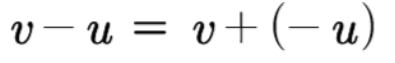
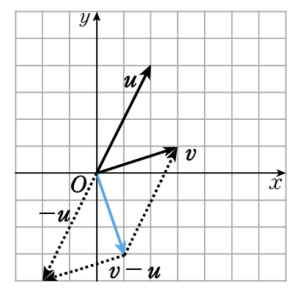
4) 벡터의 차

 

 

 

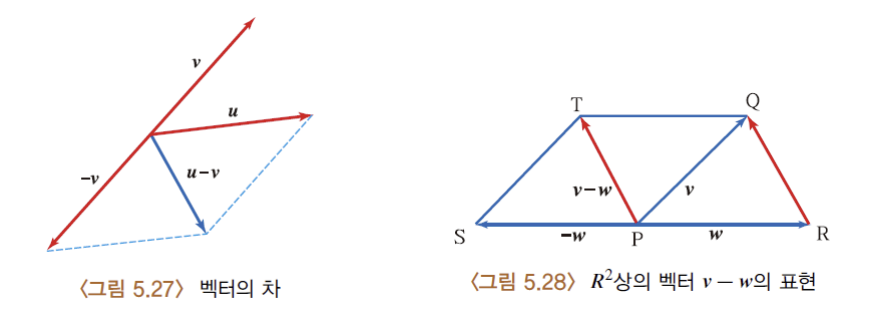
예제)

 

 

5) 벡터의 스칼라(배)곱 : 벡터를 상수배 만큼 늘리거나 줄이기

벡터 v와 스칼라 c에 대해, cv는 c에 의한 v의 스칼라배라 한다.

이는 v의 각 성분에 c를 곱한 것이다.

 

 

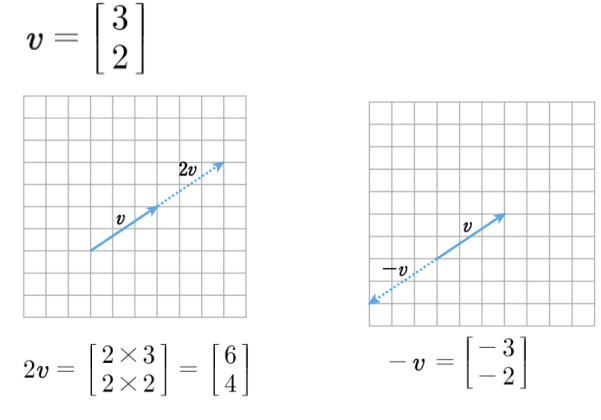
•벡터의 스칼라 곱이라는 것은 벡터를 상수배만큼 늘리거나 줄이는 것을 의미한다.

•이렇게 벡터를 늘리거나 줄인다는 의미에서 이런 과정을 Scaling(크기조정)이라고 하고,

•크기를 얼만큼 조정할지에 대한 숫자를 Scaler(스케일러=>스칼라)라고 부른다.

•그냥 수직선에서 이와 같은 연산을 한다고 봐도 이상할 것이 하나도 없다.

•그러나 대신 수직선이 X축이 아니라 XY평면상에 존재한다고만 생각하면 된다.

 

 

 

 

 

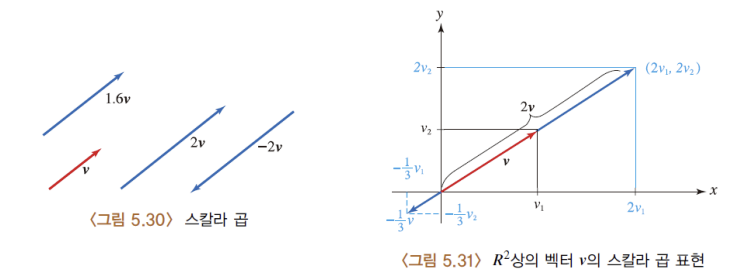
(예제)